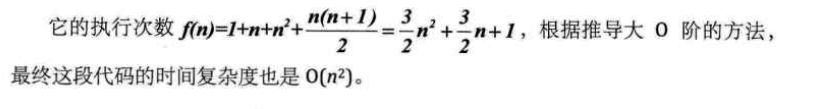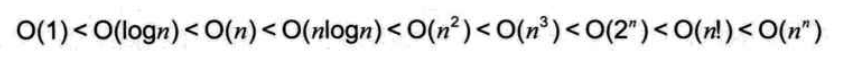算法绪论
定义
算法是解决特定问题求解步骤的描述,在计算机中为指令的有限序列,并且每一条指令表示一个或多个操作。
特性
- 有穷性
- 确定性
- 可行性
- 输入
- 输出
设计的要求
- 正确性
- 可读性
- 健壮性
- 高效率
- 低存储量
算法时间复杂度
算法时间复杂度一般用大O记法表示。一般情况下,随着n的增大,T(n)增长最慢的算法为最优算法。
推导大O阶
得到的结果就是大O阶。
常数阶
该算法的时间复杂度为 **O(1)**。
注意:
- 不管常数(即执行次数)是多少,我们都记做 **O(1)**。
- 对于分支结构,无论是真,是假,执行的次数都是恒定的。所以,单纯的分支结构(不包含在循环结构),其时间复杂度都是 **O(1)**)
线性阶
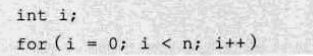
该段代码的循环的时间复杂度为 **O(n)**。因为循环体中的代码需要执行n次。
对数阶
平方阶
以上例子,是一个循环嵌套,时间复杂度为 *O(n^2)**。如果外循环次数改为m次,时间复杂度为 **O(mn)**。
因此,总结出:循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。
方法调用时的时间复杂度
上面代码调用了函数 function:
function 函数的时间复杂度是 O(1),所以整体的时间复杂度是 O(n)。
假如 function 变为下面这样的:
上述的最终的时间复杂度为 O(n^2)。
下面的代码稍微复杂一点:
对于以上复杂代码,它的分析如下:
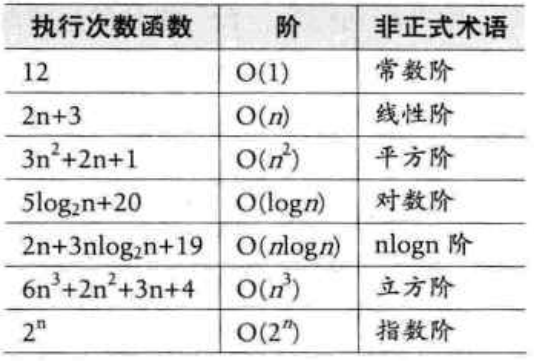
常见的时间复杂度
常用的时间复杂度所耗的时间从小到大依次是:
算法空间复杂度
线性表
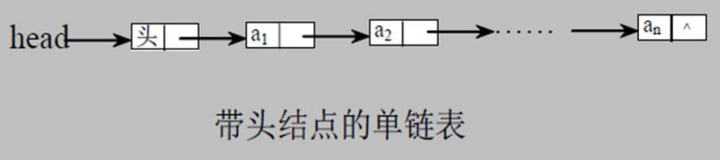
单链表
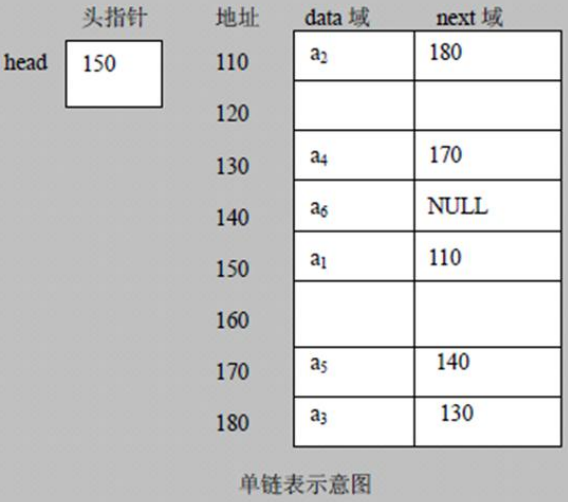
链表是有序的列表,但是它在内存中是存储如下:
小结:
- 链表是以节点的方式来存储,是链式存储
- 每个节点包含 data 域, next 域:指向下一个节点
- 如图:发现链表的各个节点不一定是连续存储
- 链表分带头节点的链表和没有头节点的链表,根据实际的需求来确定
单链表(带头结点)逻辑结构示意图如下: